1、引言

随着人们生活水平的提高以及环境意识的增强，对空气质量的要求也越来越严格，而空气净化器作为一种能够净化空气中的污染物、提高空气清洁度的设备，受到广泛的使用。空气净化器通常在室内使用，顾客对噪音有直观的体验，净化器噪声的很大一部分来自风轮与空气的作用，所以一个低噪的风轮设计就显得至关重要，对风轮进行提效和降噪优化有利于气动噪声和整体能耗的降低。本文将从空气净化器风轮着手，以降噪为首要研究目标，利用ANSYS CFD系列软件来探索一套风轮的研究方法，以作为实验的补充。

2、风轮流场仿真分析方案

市面上常见的空气净化器由过滤网、电机和风轮等组成，产品的净化原理如图1所示。

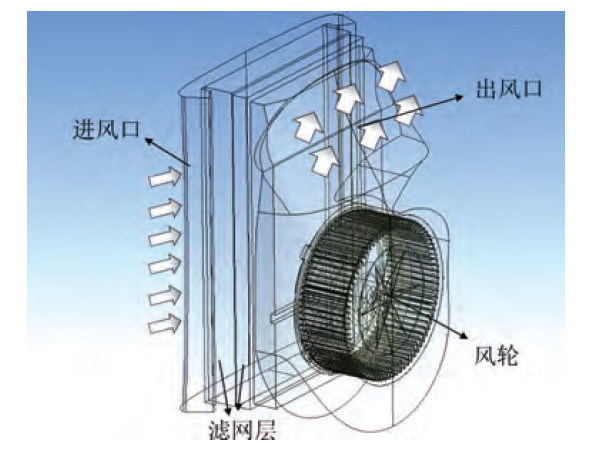
图1 空气净化器流场示意图

本文将以无限极享优乐牌空气净化器为研究对象，以现有电机、滤网等部件性能参数作为基础，利用ANSYS CFD系列软件来探索一套风轮的研究方法，对净化器的流场和噪声进行仿真优化，以达到降噪的目的，并指导后续的结构设计。

在整个空气净化器系统中，影响风轮效率及噪声大小的尺寸参数可达10多个。如果对风轮进行全参数的分析，DOE数量会非常庞大，计算周期会很长。因此在本文研究中，先保持叶型不变，选取叶轮部分安装角度和结构尺寸进行参数化分析；若降噪结果不理想，再对叶型局部参数进行优化，并进一步对叶轮安装参数进行参数优化。

3、流场及噪声优化分析

3.1 净化器流场简化及网格划分

图1为某品牌空气净化器的原始几何模型，为确保得到较高质量的网格，先通过ANSYS DM的几何清理工具，对净化器模型进行几何修复并提取流场，并进一步利用ANSYS Meshing进行网格划分，最终得到如图2所示的整体网格。

图2 净化器流场整体网格

3.2 滤网阻力模型

在空气净化器中，各层滤网起到对空气的不断过滤和净化作用，但也存在较大的空气阻力。所以在净化器流场的分析中，滤网模型必须考虑。但由于滤网层结构非常复杂，在仿真中直接进行网格划分是不现实的，对于这类结构的模拟，可使用Fluent软件的多孔介质模型来进行简化。其中初效滤网层透空率比较大且厚度较小，该层可忽略，仅需考虑HEPA微粒滤网和气味滤网，相应简化模型可根据图3和图4中压降-流速的实验数据（图中蓝色线）进行多项式拟合，最终得出两滤网的拟合关系分别为：P1=41×V1和P2=11×V2+23.5×V22，其中P1、V1表示HEPA微粒滤网的压降与流速，P2、V2表示气味滤网的压降与流速。

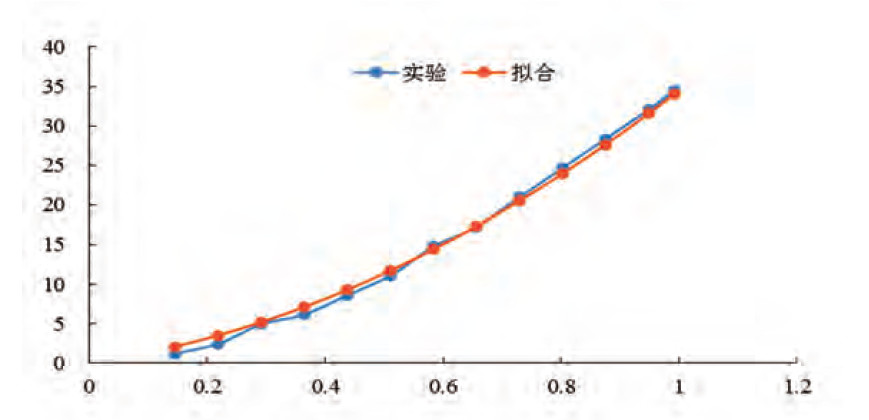
图3 HEPA微粒滤网压降-流速关系

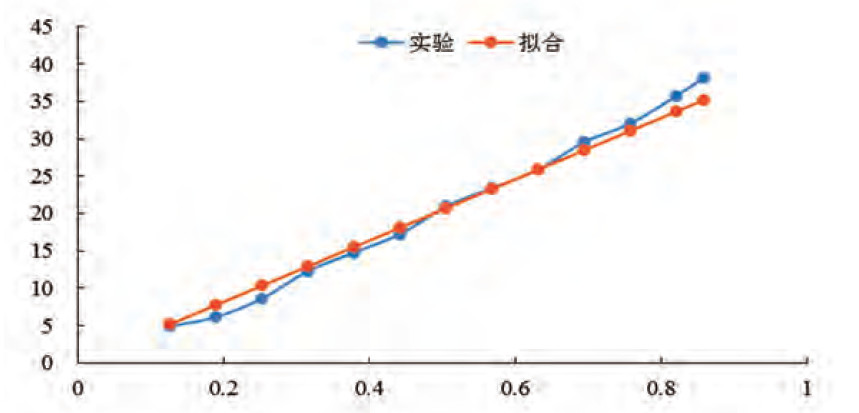
图4 气味滤网压降-流速关系

3.3 原始模型的流场及噪声评估

在进行优化计算之前，先使用FLUENT对原始模型进行分析，获得原始设计的净化空气体积流量及噪音水平，作为后续优化的基准。为提高分析效率，计算中将使用MRF的方法来模拟叶轮旋转区域，根据电机参数设定该区域转动速度为780rpm，对风机气动噪声的评估将采用FLUENT中的Proudman宽频噪声模型，主要考虑由固体边界上的湍流边界层流动产生的远场噪声，通过Curle积分评估离心风机的声功率级，在后续优化过程中比较不同方案声源最大声功率级的变化，用于评估各优化方案对噪声的影响。

计算环境工况取压力为101325Pa、温度300K时的空气参数，此时密度为1.225kg/m3；由于风道内流速较低，远小于0.3个马赫数，可认为流动是不可压的；对于该问题可设定湍流模型为SST k-w模型。通过计算最终得到空气流量为491m3/h，叶轮表面平均声功率级为45.2dB，从图5、图6中可以看到在叶轮前缘处，声功率是最大的，这可能是由于气流对叶片前缘的冲击作用引起的。

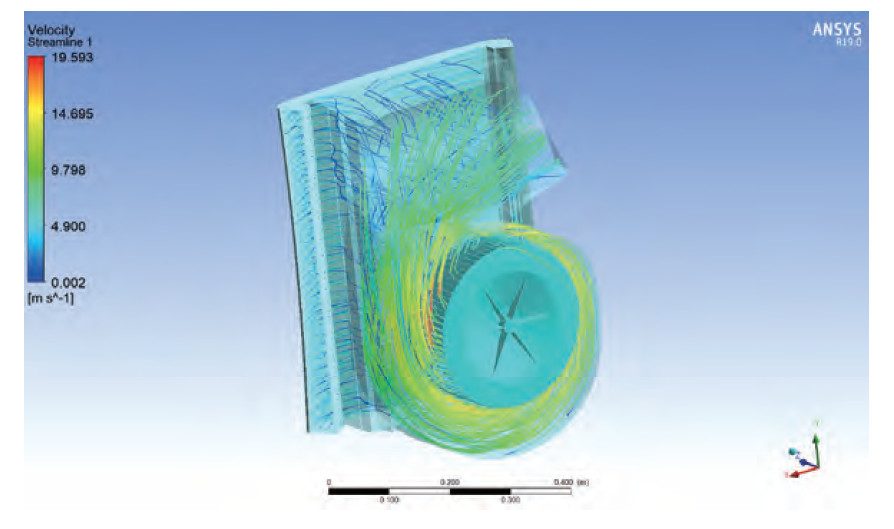
图5 速度流线图

图6 叶轮表面声功率级

3.4 风轮优化方案1

考虑到风轮的叶型和安装参数非常之多，在风轮优化方案1中将保持叶型不变，仅对以下四个参数（如图7所示，箭头方向为正）进行优化分析：

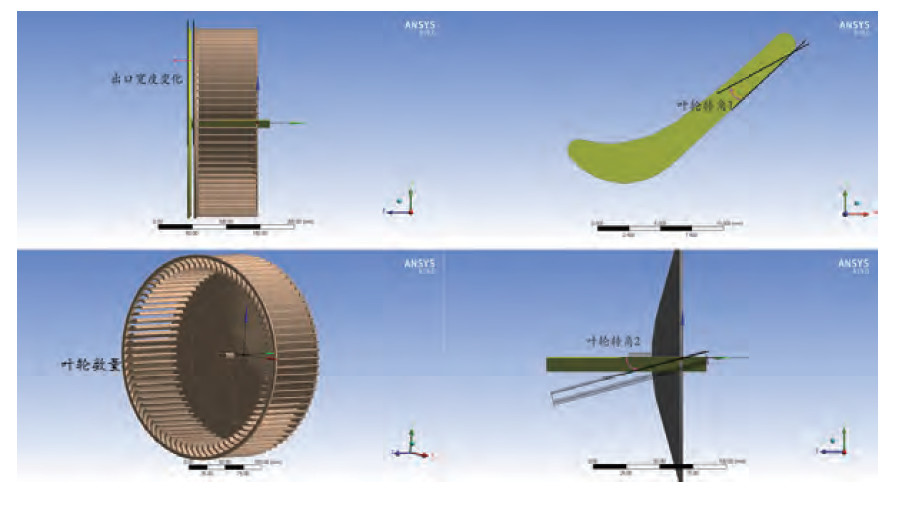
图7 叶轮参数化方案

（1）出口宽度变化：以原始宽度为基准，取值范围为[-30mm, 0mm]；

（2）叶轮转角1：叶轮扭转角度，以原设计为基准，取值范围为[-15°，15°]；

（3）叶轮转角2：叶轮倾斜角度，以原设计为基准，箭头方向为正，取值范围为[-15°，15°]；

（4）叶轮数量：取值范围为[50，80]。

确定了上述尺寸参数后，就可以进行DOE分析。DOE计算结束后，可以利用ANSYS Workbench下的Parameters Correlation工具进行全局敏感度分析，以确定在给定的参数范围内，各个输入参数对结果的影响程度，通过分析可以排除一些对结果没有影响的参数。

计算分析结果如图8，见增大出口宽度可以增加风量和全压效率，还可以减小叶轮表面最大声功率，而该参数对叶轮表面平均声功率不敏感；此外随着转角1（即叶片扭转角）变大，叶轮表面声功率会降低，但风量也会减少，而随着转角2（即叶轮倾斜角度）的增加，虽然能够提高风量，但会使得叶轮表面声功率增加；增大叶轮数量可以提高全压效率，而不会明显影响其他输出参数。

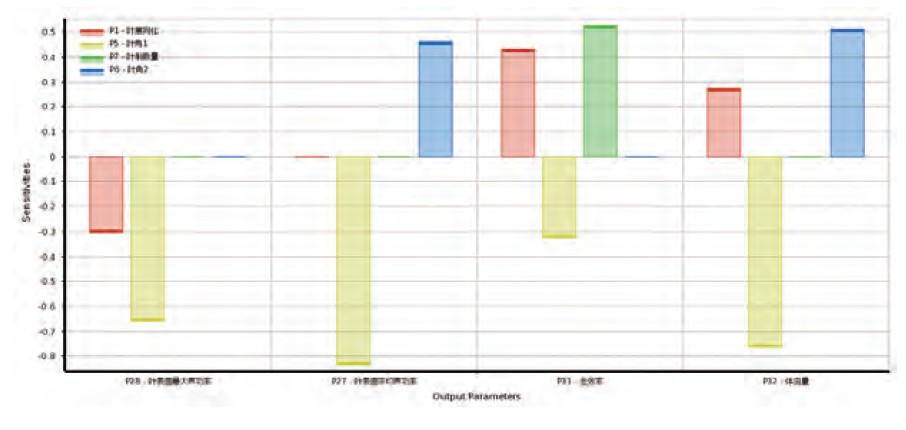
图8 风轮优化方案的全局敏感度分析图

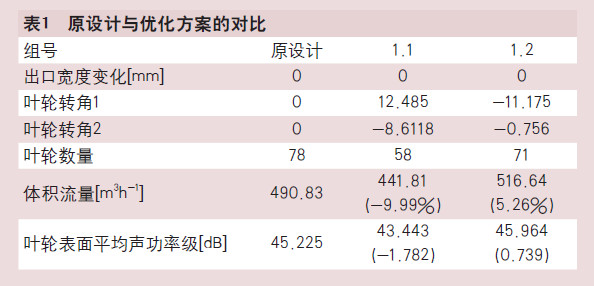
根据全局敏感性分析，出口宽度越大对高效低噪的设计更有利，考虑到空间的限制，将保持叶轮宽度不变。使用Screening方法，分别以降噪和提高流量作为主要目标进行寻优。最终得出以下原设计与优化方案的结果对比，见表1（注：以上变化均在参数取值范围内讨论），结果显示，若以降噪为优先目标，可降低叶轮表面平均声功率级约2dB，但流量也会损失10%左右；若以提高流量为优先目标，可提高流量至少5%左右，但叶轮表面平均声功率级会增加0.7dB左右。

3.5 风轮优化方案2

通过方案1的优化很难在降噪的同时进一步提高流量。因此方案2将考虑在原叶型的基础上，对叶轮局部参数进行调整，并选取较优的叶轮结构进行安装角度的优化，选取如图9的4个参数进行调整。

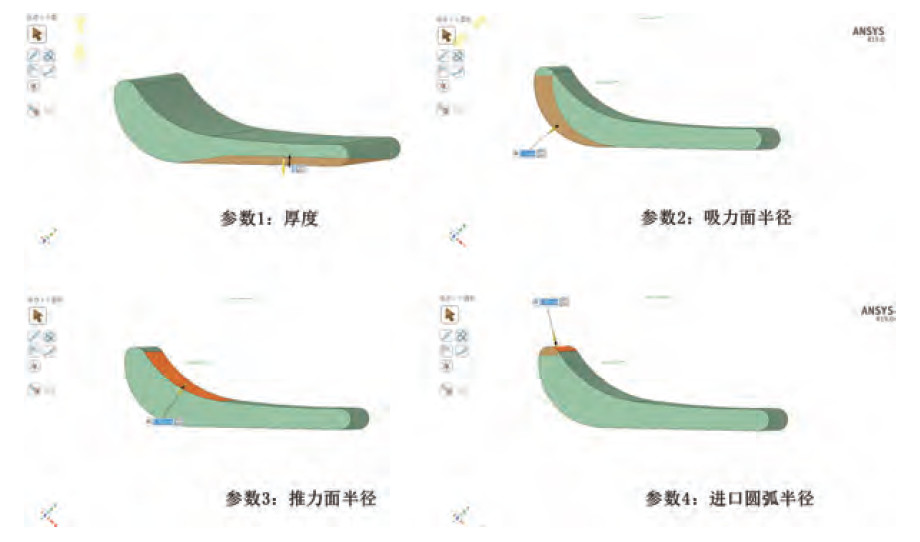
图9 局部参数优化方案

优化结果对比如表2所示，该优化后的叶轮，不仅能够提高少量流量，还能降低叶轮表面平均声功率级约0.7dB。

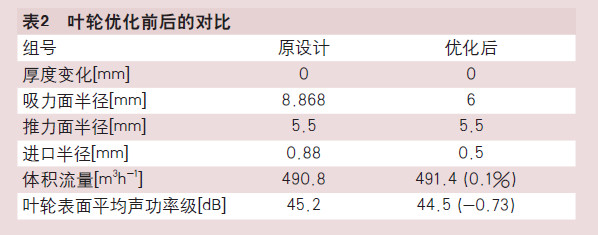
基于该优化叶轮，按照叶轮优化方案1的方法进一步进行安装角度的寻优，最终得出三种方案，见表3。

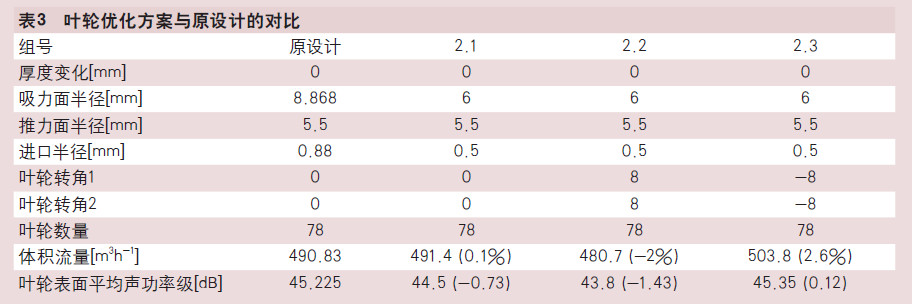
通过上述分析，由此可得组号2.2的叶轮，在流量减少不超过2%的情况下，降低叶轮表面平均声功率级达1.43dB，效果最明显。

图10为原始设计和组号2.2的流线图对比，可见流线的倾斜分布与叶轮的倾斜布置更加匹配，另外可以明显降低叶轮流道内的涡流区域，最终提高出风的效率。

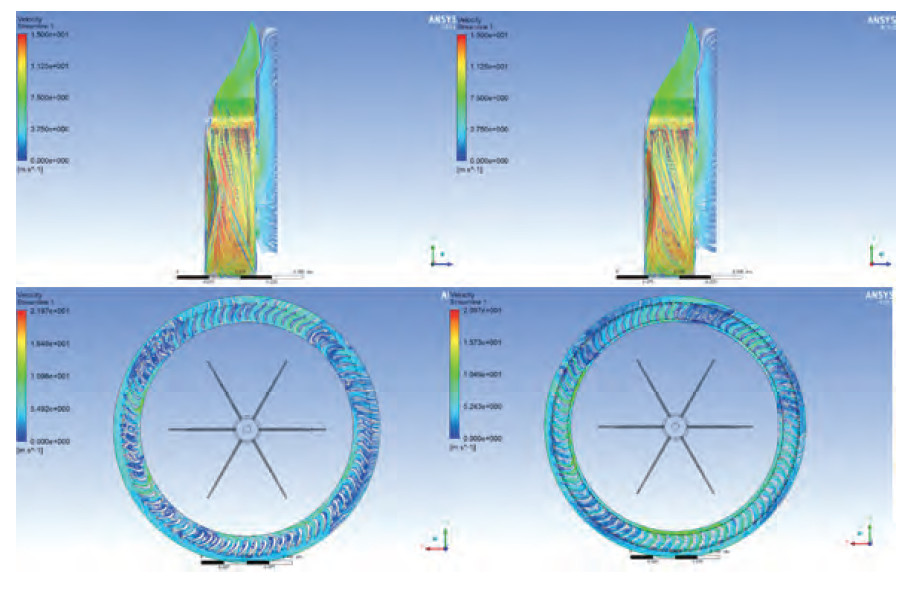
图10 原始设计（左）和组号2.2（右）的流线图

4、实验结果

为验证仿真优化方案的可行性，针对原风轮和按照方案组号2.2优化后的风轮结构，采用家用电器噪声测试标准GB/T 4214.1-2000中提供的方法，分别进行了净化器的噪声测试，相应的测试结果如表4。

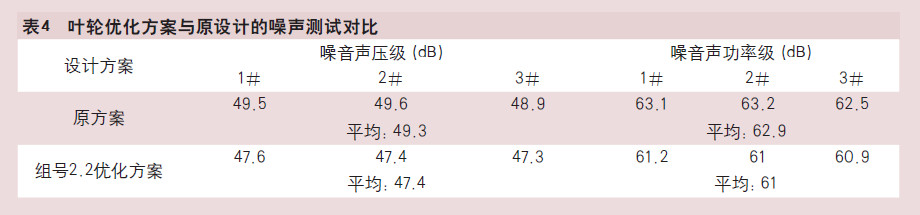
由测试结果可知，通过风轮的优化，最后能降低噪声约1.9dB，与CFD降噪分析趋势一致，说明利用该参数优化方法进行降噪研究是可行的。

5、结论

本文通过ANSYS Workbench平台来搭建自动化，参数化分析及优化流程，利用DesignXplorer软件研究了风轮设计参数对流量和噪声等输出参数的影响，结果显示通过结构优化可以达到降噪的目的，并通过试验验证了该方法的可靠性。主要的结论如下：

（1）通过对风轮安装角度进行参数优化，以降噪为优先目标，可降低叶轮表面平均声功率级约2dB，但流量也会损失10%左右；若以提高流量为优先目标，可提高流量至少5%左右，但叶轮表面平均声功率级会增加0.7dB左右。

（2）通过对风轮局部参数进行优化，以降噪和提高流量作为综合目标进行寻优，最终得到了可以同时提高流量和降低噪声的叶轮设计，并且进一步对安装角度进行参数调整，最终得到了一组叶轮方案，在不明显降低出风量的情况下，能减少叶轮表面声功率级达1.43dB。

（3）总的来说，对该类型的离心风轮，在不改变原风机结构的情况下，根据输出目标的不同，可以参考表5去调整尺寸参数，可见，要达到高效低噪的目的，通常有两种办法：一是根据实际情况来折中选择，这也是目前DesignXplorer软件常用的寻优方法；二是通过优化风道参数来达到高效低噪的目的，这也是下一阶段将进行的研究。

参考文献

[1] 叶建雄, 周金兰, 牛尚斌, 郭磊. 空气净化器净化及控制技术发展[J]. 日用电器, 2018(02):57-59.

[2] 李佳, 刘震涛, 刘忠民, 谭永南, 俞小莉. 空气滤清器流动过程仿真与试验分析[J]. 浙江大学学报(工学版), 2012,46(02):327-332.

[3] 朱正权, 陆金桂, 尹振华, 夏正雷. 基于CFD的汽车空气调节系统离心风机流场与气动噪声数值模拟[J]. 轻工学报, 2018,33(03):101-108.

[4] 邵双全, 邹慧明, 徐洪波, 田长青, 孙鹏, 桑宇宁. 基于CFD仿真的双工况多翼离心风机优化设计[J]. 制冷技术, 2014,34(06):13-16.